SPLDV
Contoh Soal 1
Beni, Udin, dan Citra pergi ke toko buku “Cerdas”. Beni membeli 4 buku tulis dan 3 pensil dengan harga Rp 12.500,00 dan Udin membeli 2 buku tulis dan sebuah pensil dengan harga Rp 5.500,00 pada toko yang sama. Tentukan harga yang harus dibayar Citra jika ia membeli 6 buku tulis dan 2 pensil!
Penyelesaian:
Misalkan harga buku = x dan harga pensil = y.
Belajaan Beni akan memenuhi persamaan:
4x + 3y = 12500
Belajaan Udin akan memenuhi persamaan:
2x + y = 5500
Diperoleh SPLDV yakni:
4x + 3y = 12500 . . . . pers (1)
2x + y = 5500 . . . . pers (2)
Adapun metode yang akan dipilih dalam menyelesaikan SPLTV yakni metode subtitusi.
Langkah I
Ubah persamaan 2 yakni:
2x + y = 5500
y = 5500 – 2x . . . . pers (3)
Langkah II
Subtitusi persamaan 3 ke persamaan 1, maka:
4x + 3y = 12500
4x + 3(5500 – 2x) = 12500
4x + 16500 – 6x = 12500
– 2x = – 4000
x = 2000
Langkah III
Substitusi nilai x ke persamaan 3, maka:
y = 5500 – 2x
y = 5500 – 2(2000)
y = 5500 – 4000
y = 1500
Jadi harga sebuah buku tulis Rp 2000,00 dan harga sebuah pensil Rp 1500,00.
Langkah IV
Harga yang harus dibayar Citra yakni:
Harga = 6x + 2y
Harga = 6(2000) + 2(1500)
Harga = 12000 + 3000
Harga = 15000
Jadi, harga total yang harus dibayar Citra adalah Rp 15.000,00
Contoh Soal 2
Sebuah rakit terbuat dari bambu yang bergerak searah arus sungai dapat menempuh jarak 46 km dalam 2 jam. Jika rakit tersebut bergerak berlawanan dengan arah arus sungai dapat menempuh jarak 51 km dalam 3 jam. Berapa kecepatan aliran air sungai dan kecepatan rakit?
Penyelesaian:
Misalkan kecepatan arus sungai = a, dan kecepatan rakit = b.
Jika bergerak searah arus sungai memenuhi persamaan:
a + b = 46/2 => a + b = 23
Jika bergerak berlawanan arah arus sungai memenuhi persamaan:
a – b = 51/3 => a – b = 17
Diperoleh SPLDV yakni:
a + b = 23 . . . . pers (1)
a – b = 17 . . . . pers (2)
Adapun metode yang akan dipilih dalam menyelesaikan SPLTV ini bisa menggunakan metode eliminasi.
Langkah I
Eliminasi b pada persamaan 1 dan 2 yakni:
a + b = 23
a – b = 17
------------- +
2a = 40
a = 20
Langkah II
Eliminasi a pada persamaan 1 dan 2 yakni:
a + b = 23
a – b = 17
------------- -
2b = 6
b = 3
Jadi, kecepatan aliran air sungai dan kecepatan rakit adalah 20 km/jam dan 3 km/jam.
Contoh Soal 3
Tarif tiket masuk ke tempat wisata pantai Pandawa di Bali untuk 2 orang dewasa dan tiga orang anak-anak adalah Rp 28.000,00 dan untuk 3 orang dewasa dan empat orang anak-anak adalah Rp 40.000,00. Jika sepasang suami istri dan dua orang anaknya akan berpergian ke tempat wisata pantai Pandawa, berapakah total harga tiket yang harus mereka bayar?
Penyelesaian:
Misalkan tarif tiket masuk untuk dewasa = x dan untuk anak-anak = y, maka memenuhi persamaan SPLDV yakni:
2x + 3y = 28000 . . . pers (1)
3x + 4y = 40000 . . . pers (2)
2x + 2y = . . . ?
Adapun metode yang akan dipilih dalam menyelesaikan SPLTV ini bisa menggunakan metode campuran (gabungan metode eliminasi dengan metode subtitusi).
Langkah I
Eliminasi x dengan menyamakan koefesien x pada persamaan 1 dan 2 terlebih dahulu, maka:
2x + 3y = 28000 x3
3x + 4y = 40000 x2
6x + 9y = 84000
6x + 8y = 80000
--------------------- -
y = 4000
Langkah II
Subtitusi nilai y ke persamaan 1, yakni:
2x + 3y = 28000
2x + 3(4000) = 28000
2x + 12000 = 28000
2x = 16000
x = 8000
Jadi harga tiket masuk untuk dewasa adalah Rp 8.000,00 dan untuk anak-anak adalah Rp 4.000,00
Langkah III
Bayar = 2x + 2y
Bayar = 2(8000) + 2(4000)
Bayar = 16000 + 8000
Bayar = 24000
Jadi, total harga tiket yang harus mereka bayar adalah Rp 24.000,00
----------------------------------------------------------------------------------------------------
Contoh soal SPLDV menggunakan metode grafik
Adapun langkah-langkah untuk menyelesaikan SPLDV dengan metode grafis adalah sebagai berikut.
Langkah 1:
■ Tentukan koordinat titik potong masing-masing persamaan terhadap sumbu-X dan sumbu-Y.
■ Gambarkan grafik dari masing-masing persamaan pada sebuah bidang Cartesius.
Langkah 2:
■ Jika kedua garis berpotongan pada satu titik, maka himpunan penyelesaiannya tepat memiliki satu anggota.
■ Jika kedua garis sejajar, maka himpunan penyelesaiannya tidak memiliki anggota. Dikatakan himpunan penyelesaiannya adalah himpunan kosong, dan ditulis ∅.
■ Jika kedua garis saling berhimpit, maka himpunan penyelesaiannya memiliki anggota yang tak hingga banyaknya.
Contoh soal 4
Apabila hasil penjualan seluruh karcis Rp 3.250.000,00, maka tentukan banyak karcis masing-masing kelas I dan II yang terjual.
Langkah pertama ialah mengubah kalimat-kalimat pada soal cerita di atas menjadi model matematika, sehingga membentuk sistem persamaan linear.
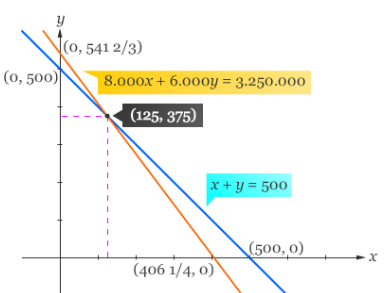
Jika terjualnya karcis secara berturut yakni x dan y, maka kalimat “dalam sebuah konser , terjual karcis kelas I dan kelas II sebanyak 500 lembar,” dapat dimodelkan menjadi, x+y=500
Sedangkan grafik 8.000x + 6.000y = 3.250.000 memotong sumbu-x di (406 1/4, 0) dan memotong sumbu-y di (0, 541 2/3).
Langkah ketiga, kita gambarkan grafik persamaan tersebut pada koordinat Cartesius. Maka dari Grafik di atas dapat dilukis dengan memplot titik dikordinat Cartesius kemudian hubungkan titik (500, 0) dan (0, 500) untuk mendapatkan grafik x + y = 500, serta titik (406 1/4, 0) dan (0, 541 2/3) untuk mendapatkan grafik 8.000x + 6.000y = 3.250.000.
Dari grafik di atas diperoleh bahwa titik potong grafik x + y = 500 dan 8.000x + 6.000y = 3.250.000 ialah (125, 375). Sehingga selesaian dari SPLDV di atas ialah x = 125 dan y = 375.
Langkah keempat, dengan menggunakan penyelesaian di atas guna menjawab pertanyaan pada soal cerita. Dalam hal tersebut disebabkan oleh x dan y yang secara berturut menyatakan banyaknya karcis I dan II yang terjual, yakni 125 lembar dan 375 lembar
Nirinna Afliyah Nisrin. 2021. SPLDV
Sumber : https://mafia.mafiaol.com/2020/10/contoh-soal-cerita-sistem-persamaan-linear-dua-variabel-spldv.html?m=1
https://yos3prens.wordpress.com/2013/09/29/menyelesaikan-spldv-dengan-metode-grafik/



Komentar
Posting Komentar